Masala #R018D
Maksimum uzunlik
Quyidagidek belgilash kiritaylik.
edge (rus tilida “Ребро”) – a va b orasida edge bor degani – a va b shaharlar orasida to’g’ridan – to’g’ri ikki tomonli yo’l bor degani. Ya’ni a va b qo’shni shaharlar. Har bir edgening uzunligi 1 km.
path (rus tilida “Путь”) – a dan b ga boradigan path degani – a shahardan b shaharga boruvchi eng qisqa yo’l (bir yoki bir nechta edgedan o’tuvchi eng qisqa yo’l). Pathning uzunligi deb, ushbu path nechta edgedan o’tganiga aytiladi. Yoki a va b orasidagi masofa.
Masalan rasmda 1 va 4 orasida edge bor hamda 2 va 5 orasida edge bor. Yoki 3 va 5 orasidagi pathning uzunligi 3ga teng.
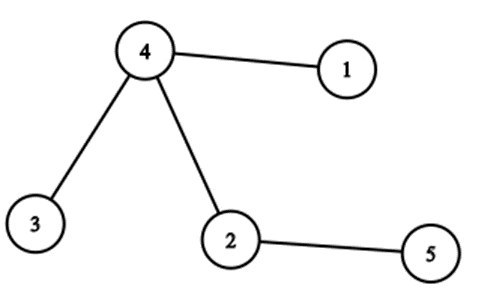
Baytlandiyada n ta shahar bor. Ular orasida n-1 ta edge bor. Ixtiyoriy shahardan boshqa bir shaharga faqat bitta path bor. Sizga q ta so’rov va har bir so’rovda x natural soni beriladi. Sizning vazifangiz x-shahardan eng uzoqda joylashgan shahardan x ga eng yaqin bo’lgan shaharlar orasidagi pathning uzunligi maximum nechi bo’lishi mumkin? Masalan, x dan eng uzoqda joylashgan shaharlardan biri a bo’lsin, x ga eng yaqin joylashgan shaharlardan biri b bo’lsin. U holda a dan b ga boruvchi pathning uzunligi eng ko’pi bilan nechi bo’lishi mumkin?
Masala shartiga tushunmaganlar uchun avval graflar teoriyasi hamda daraxtlar haqida o’qib chiqish tavsiya etiladi:
Graflar teoriyasi
Daraxtlar
Bitta qatorda n va q butun sonlar. (2 ≤ n ≤ 2×105, 1 ≤ q ≤ 2×105). Shaharlar 1 dan n gacha raqamlangan.
Keyingi n-1 ta qatorda ikkitadan butun a va b sonlari – a va b shaharlar orasida edge, ikki tomonli to’g’ridan – to’g’ri yo’l bor degani. (1 ≤ a, b ≤ n).
Keyingi q ta qatorda bittadan x butun son. (1 ≤ x ≤ n)
Har bitta so’rov uchun alohida qatorda bittadan butun son – x ga eng yaqin shahardan x dan eng uzoqdagi shahargacha masofalarning maximali.
| # | input.txt | output.txt |
|---|---|---|
| 1 |
5 2 1 4 4 2 4 3 2 5 2 1 |
3 2 |
2 dan eng uzoqdagi shahar 1, eng yaqini 5 bo’lganda javob maximal bo’ladi. 1 dan 5 gacha masofa 3 ga teng.